SCI Publications
2008
L.T. Tran, J. Kim, M. Berzins.
“An Introduction to the Material Point Method using a Case Study from Gas Dynamics,” In Numerical Analysis and Applied Mathematics: International Conference on Numerical Analysis and Applied Mathematics 2008. AIP Conference Proceedings, Vol. 1048, Edited by T.E. Simos and G. Psihoyios and Ch. Tsitouras, pp. 26--29. 2008.
ISBN: 978-0-7354-0576-9
X. Tricoche, R.S. MacLeod, C.R. Johnson.
“Visual Analysis of Bioelectric Fields,” In Visualization in Medicine and Life Sciences, Mathematics and Visualization, Springer-Verlag, pp. 205--220. 2008.
J.K. Triedman, M. Jolley, J. Stinstra, D.H. Brooks, R.S. MacLeod.
“Predictive Modeling of Defibrillation Using Hexahedral and Tetrahedral Finite Element Models: Recent Advances,” In Journal of Electrocardiology, Vol. 41, pp. 483--486. 2008.
S. Vakkalanka, M. DeLisi, G. Gopalakrishnan, R.M. Kirby, R. Thakur, W. Gropp.
“Implementing Efficient Dynamic Formal Verification Methods for MPI Programs,” In Recent Advances in Parallel Virtual Machine and Message Passing Interface
Lecture Notes in Computer Science, Dublin, Ireland, Vol. 5205, pp. 248--256. September, 2008.
We examine the problem of formally verifying MPI programs for safety properties through an efficient dynamic (runtime) method in which the processes of a given MPI program are executed under the control of an interleaving scheduler. To ensure full coverage for given input test data, the algorithm must take into consideration MPI’s out-of-order completion semantics. The algorithm must also ensure that nondeterministic constructs (e.g., MPI wildcard receive matches) are executed in all possible ways. Our new algorithm rewrites wildcard receives to specific receives, one for each sender that can potentially match with the receive. It then recursively explores each case of the specific receives. The list of potential senders matching a receive is determined through a runtime algorithm that exploits MPI’s operation ordering semantics. Our verification tool ISP that incorporates this algorithm efficiently verifies several programs and finds bugs missed by existing informal verification tools.
S. Vakkalanka, M. DeLisi, G. Gopalakrishnan, R.M. Kirby.
“Scheduling Considerations for Building Dynamic Verification Tools for MPI,” In Proceedings of the 6th Workshop on Parallel and Distributed Systems: Testing, Analysis, and Debugging, Seattle, WA, PADTAD '08, Vol. 3, ACM, pp. 1--6. 2008.
ISBN: 978-1-60558-052-4
DOI: 10.1145/1390841.1390844
S. Vakkalanka, G. Gopalakrishnan, R.M. Kirby.
“Dynamic Verification of MPI Programs with Reductions in Presence of Split Operations and Relaxed Orderings,” In Computer Aided Verification Lecture Notes in Computer Science , Vol. 5123, pp. 66--79. July, 2008.
DOI: 10.1007/978-3-540-70545-1_9
Dynamic verification methods are the natural choice for debugging real world programs when model extraction and maintenance are expensive. Message passing programs written using the MPI library fall under this category. Partial order reduction can be very effective for MPI programs because for each process, all its local computational steps, as well as many of its MPI calls, commute with the corresponding steps of all other processes. However, when dependencies arise among MPI calls, they are often a function of the runtime state. While this suggests the use of dynamic partial order reduction (DPOR), three aspects of MPI make previous DPOR algorithms inapplicable: (i) many MPI calls are allowed to complete out of program order; (ii) MPI has global synchronization operations (e.g., barrier) that have a special weak semantics; and (iii) the runtime of MPI cannot, without intrusive modifications, be forced to pursue a specific interleaving because of MPI’s liberal message matching rules, especially pertaining to ‘wildcard receives’. We describe our new dynamic verification algorithm ‘POE’ that exploits the out of order completion semantics of MPI by delaying the issuance of MPI calls, issuing them only according to the formation of match-sets, which are ample ‘big-step’ moves. POE guarantees to manifest any feasible interleaving by dynamically rewriting wildcard receives by specific-source receives. This is the first dynamic model-checking algorithm with reductions for (a large subset of) MPI that guarantees to catch all deadlocks and local assertion violations, and is found to work well in practice.
S.X. Vasquez, M.S. Hansen, A.N. Bahadur, M.F. Hockin, G.L. Kindlmann, L. Nevell, I.Q. Wu, D.J. Grunwald, D.M. Weinstein, G.M. Jones, C.R. Johnson, J.L. Vandeberg, M.R. Capecchi, C. Keller.
“Optimization of Volumetric Computed Tomography for Skeletal Analysis of Model Genetic Organisms,” In The Anatomical Record: Advances in Integrative Anatomy and Evolutionary Biology, Vol. 291, pp. 475--487. 2008.
PubMed ID: 18286615
A.I. Veress, J.A. Weiss, R.H. Huesman, B.W. Reutter, S.E . Taylor, A. Sitek, B. Feng, Y. Yang, G.T. Gullberg.
“Measuring Regional Changes in the Diastolic Deformation of the Left Ventricle of SHR Rats Using MicroPET Technology and Hyperelastic Warping,” In Annals of Biomedical Engingeering, Vol. 36, No. 7, pp. 1104--1017. 2008.
K. Vieira, L. Barbosa, J. Freire, A. Silva.
“Siphon++: A Hidden-Web Crawler for Keyword-Based Interfaces,” In Proceeding of the 17th ACM conference on Information and knowledge management (CIKM), pp. 1361--1362. November, 2008.
I. Wald, T. Ize, S.G. Parker.
“Fast, Parallel, and Asynchronous Construction of BVHs for Ray Tracing Animated Scenes,” In Computers and Graphics, Vol. 32, No. 1, pp. 3--13. February, 2008.
H. Wang, C.E. Scheidegger, C.T. Silva.
“Optimal Bandwidth Selection for MLS Surfaces,” In IEEE International Conference on Shape Modeling and Applications (SMI) 2008, pp. 111--120. 2008.
ISBN: 978-1-4244-2260-9
DOI: 10.1109/SMI.2008.4547957
R.T. Whitaker, R.M. Kirby, J.G. Sinstra, M.D. Meyer.
“Multimaterial Meshing of MRI Head Data for Bioelectric Field Simulations,” In Proceedings of the 17th International Meshing Roundtable, 2008.
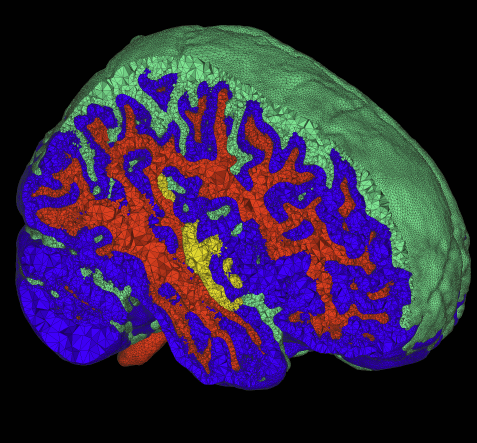
The problem of body fitting meshes that are both adaptive and geometrically accurate is important in a variety of biomedical applications in a multitude of clinical settings, including electrocardiology, neurology, and orthopedics. Adaptivity is necessary because of the combination of large-scale and smallscale structures (e.g. relatively small blood vessels spanning a human head). Geometric accuracy is important for several reasons. In some cases, such as computational fluid dynamics, the fine-scale structure of the fluid domain is important for qualitative and quantitative accuracy of the solutions. More generally, finite element approximations of elliptic problems with rough coefficients require increased spatial resolution normal to material boundaries [3]. The problem of constructing meshes from biomedical images is particularly difficult because of the complexity and irregularity of the structures, and thus tuning or correcting meshes by hand is quite difficult and time consuming. Many researchers and, indeed, commercial products simply subdivide the underlying hexahedral image grid and assign material properties to tetrahedra based on standard decomposition of each hexahedron into tetrahedra.
This paper presents a small case study of the results of a recently developed method for multimaterial, tetrahedral meshing of biomedical volumes [6]. The method uses an iterative relaxation of surface point point positions that are constrained to subsets of the volume that correspond to boundaries between different materials. In this paper we briefly review the method and present results on a set of MRI head images for use in bioelectric field simulation and source localization.
D. Xiu.
“Numerical Integration Formulas of Degree Two,” In Applied Numerical Mathematics, Vol. 58, No. 10, pp. 1515--1520. 2008.
DOI: 10.1016/j.apnum.2007.09.004
Numerical integration formulas in n-dimensional nonsymmetric Euclidean space of degree two, consisting of n+1 equally weighted points, are discussed, for a class of integrals often encountered in statistics. This is an extension of Stroud's theory [A.H. Stroud, Remarks on the disposition of points in numerical integration formulas, Math. Comput. 11 (60) (1957) 257–261; A.H. Stroud, Numerical integration formulas of degree two, Math. Comput. 14 (69) (1960) 21–26]. Explicit formulas are given for integrals with nonsymmetric weights. These appear to be new results and include the Stroud's degree two formula as a special case.
Keywords: Numerical integration, Cubature formulas
S. Xu, M. Styner, J.H. Gilmore, G. Gerig.
“Multivariate Longitudinal Statistics for Neonatal-Pediatric Brain Tissue Development,” In Proceedings of SPIE Medical Imaging 2008, Vol. 6914, February, 2008.
DOI: 10.1117/12.773966
The topic of studying the growth of human brain development has become of increasing interests in the neuroimaging community. Cross-sectional studies may allow comparisons between means of different age groups, but they do not provide any growth model that integrates the continuum of time, nor do they present any information about how individuals/population change over time. Longitudinal data analysis method arises as a strong tool to address these questions. In this paper, we use longitudinal analysis methods to study tissue development in early brain growth; a novel approach of multivariate longitudinal analysis is applied to study the associations between the growth of different brain tissues. We present in this paper the methodologies to statistically study scalar (univariate) and vector (multivariate) longitudinal data, and our exploratory results in the study of neonatal-pediatric brain tissue development. We obtained growth curves as a quadratic function of time for all three tissues. The quadratic terms were then tested to be statistically signicant, showing that there was indeed a quadratic growth of tissues in early brain development. Moreover, our result shows that there is a positive correlation between repeated measurements of any single tissue, and among those of different tissues. Our approach is generic in natural and thus can be applied to any longitudinal data with multiple outcomes, even brain structures. Also, our joint mixed model is flexible enough to allow incomplete and unbalanced data, i.e. subjects do not need to have the same number of measurements, or be measured at the exact time points.
Keywords: ucnia
S. Xu, M. Styner, J. Gilmore, J. Piven, G. Gerig.
“Multivariate Nonlinear Mixed Model to Analyze Longitudinal Image Data: MRI Study of Early Brain Development,” In Proceedings of IEEE Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA) 2008, IEEE Computer Society, pp. 1--8. June, 2008.
ISBN: 978-1-4244-2339-2
DOI: 10.1109/CVPRW.2008.4563011
Y. Yang, X. Chen, G. Gopalakrishnan, R.M. Kirby.
“Efficient Stateful Dynamic Partial Order Reduction,” In Proceedings of Model Checking Software: 15th International SPIN Workshop, Los Angeles, CA, Vol. 5156, pp. 288--305. August, 2008.
DOI: 10.1007/978-3-540-85114-1_20
In applying stateless model checking methods to realistic multithreaded programs, we find that stateless search methods are ineffective in practice, even with dynamic partial order reduction (DPOR) enabled. To solve the inefficiency of stateless runtime model checking, this paper makes two related contributions. The first contribution is a novel and conservative light-weight method for storing abstract states at runtime to help avoid redundant searches. The second contribution is a stateful dynamic partial order reduction algorithm (SDPOR) that avoids a potential unsoundness when DPOR is naively applied in the context of stateful search. Our stateful runtime model checking approach combines light-weight state recording with SDPOR, and strikes a good balance between state recording overheads, on one hand, and the elimination of redundant searches, on the other hand. Our experiments confirm the effectiveness of our approach on several multithreaded benchmarks in C, including some practical programs.
S. Yau, K. Damevski, D. Zorin, V. Karamcheti, S.G. Parker.
“Result Reuse in Design Space Exploration: A Study in System Support for Interactive Parallel Computing,” In Proceedings of the 22nd International Parallel and Distributed Processing Symposium (IPDPS 2008), Miami, Florida, pp. 1--12. 2008.
F. Zhang, E.R. Hancock, C. Goodlett, G. Gerig.
“Probabilistic White Matter Fiber Tracking using, Particle Filtering and von Mises-Fisher Sampling,” In Medical Image Analysis (MedIA), pp. (in print). 2008.
2007
G. Adluru, S.P. Awate, T. Tasdizen, R.T. Whitaker, E.V.R. DiBella.
“Temporally Constrained Reconstruction of Dynamic Cardiac Perfusion MRI,” In Magnetic Resonance in Medicine, Vol. 57, pp. 1027--1036. 2007.
G. Adluru, R.T. Whitaker, E.V.R. DiBella.
“Spatio-Temporal Constrained Reconstruction of Sparse Dynamic Contrast Enhanced Radial MRI Data,” In Proceedings of the IEEE International Symposium on Biomedical Imaging, pp. 109--112. 2007.
Page 83 of 144
