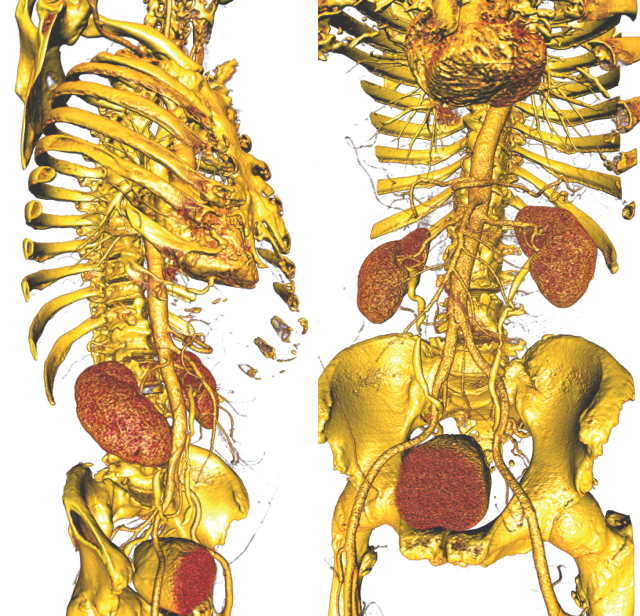
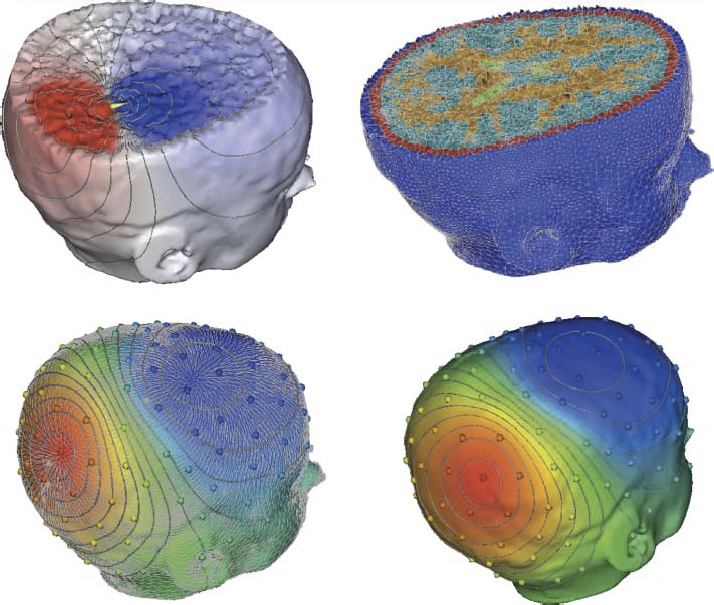
|
A "typical" workflow that applies to many problems in biomedical simulation contains the following elements: (i) Image acquisition and processing for a tissue, organ or region of interest (imaging and image processing), (ii) Identification of structures, tissues, cells or organelles within the images(image processing and segmentation), (iii) Fitting of geometric surfaces to the boundaries between structures and regions (geometric modelling), (iv) Generation of three-dimensional volume mesh from hexahedra or tetrahedra (meshing), and (v) Application of tissue parameters and boundary conditions and computation of spatial distribution of scalar, vector or tensor quantities of interest (simulation). |
Many simulation studies in biomedicine are based on a similar sequence of processing steps, starting from images and running through geometric model generation, assignment of tissue properties, numerical simulation and visualization of the results—a process known as image-based geometric modeling and simulation. In recent publications we have presented an overview of software systems for implementing such a sequence both within highly integrated problem-solving environments and in the form of loosely integrated pipelines. Our approach has been something of a hybrid using elements of both top-down design and bottom-up design. As an example of the top-down approach, we continue to use and expand SCIRun, a very general purpose problem-solving environment, to test algorithms and approaches and develop application-specific solutions. SCIRun is a stable platform that exhibits many of the advantages of the top-down design strategy - data structures and APIs are consistent and predictable and there is a high degree of code sharing and usefulness of capabilities developed previously. Using SCIRun greatly simplifies interactive visualization and steering of the process because of pre-existing capabilities and provides extensive support for the simulation component of the project. However, the interface to SCIRun is complex for a biological user and even the nomenclature of the user interface elements is quite computer technical rather than biomedical. As a result, the burden of setting up and carrying out the simulations often falls more to the technical members of the team than to the biomedical collaborator. We have also followed the complementary, bottom-up approach of developing a small, focused and standalone software system for tasks that are ubiquitous across many projects. Our oldest example of this strategy is map3d, which is an interactive visualization program created for multichannel time signals whose spatial organization is in surfaces. The program has a highly focused set of technical capabilities and the application domain has traditionally been cardiac or neural electrophysiology. The program is also the creation of a very small team, one of whom is a biomedical scientist so that the interface and the nomenclature are familiar and easily adopted by the target community.
Implementation of the pipeline
Top-down approach
We have implemented within SCIRun several meshing and mesh refinement schemes based on hexahedral and tetrahedral elements and used them extensively in the example of simulation of cardiac defibrillation. Most of these meshing schemes start by overlaying a regular grid on top of the voxelized images and then turning them into a model by adding local refinements and boundaries based on the needs of the simulation. Although carrying out refinement to an existing mesh is a relatively straightforward task, it becomes much more challenging when maintaining good mesh quality, i.e. controlling the shape and size of the elements. In biological problems, meshes often require embedding of irregularly shaped boundaries of different tissue properties as well as adding local refinements for detailed simulations around biological sources. We have developed novel methods to approximate such features using hexahedral meshes that also allow the addition of irregular boundaries while still maintaining high mesh quality.Bottom-up approach
The key to benefitting from the bottom-up approach is creating efficient and flexible elemental pieces that can interact through simple passing of data via files. Pipeline structures, in general, lend themselves well to this concept and we have implemented image-based modeling pipelines from such elements. Elements of this strategy include ImageVis3D and Seg3D (www.seg3d.org), which provide volume rendering and segmentation capabilities, respectively. ImageVis3D is based on our own volume rendering capabilities and Seg3D uses tools from the ITK (www.itk.org) and has a relatively focused technical breadth. Seg3D reads stacks of images as a volume using standard file formats and provides a set of tools to identify different regions within the image volume and thus generate a 'label map' of the volume.The nomenclature of both ImageVis3D and Seg3D is largely generic and not specific to any particular application domain and both are small programs, created within a year by a small team with the goal of facilitating rapid addition of new features or adjustments to the user interface. While these are separate programs, they integrate functionally into the workflow through files, which they can flexibly read and write.
In some applications, we have also used a second segmentation tool, 3D Slicer (www.slicer.org), which is part of the NA-MIC kit. Although Slicer is much more than a segmentation program, it is also portable and flexible enough to serve as a dedicated segmentation tool in the simulation pipeline. Integration occurs, as with Seg3D, by means of compatible file formats using the Nearly Raw Raster Data (NRRD) format and the associated TEEM toolkit for accessing and writing NRRD files.
 |
 |
| Figure from R.S. MacLeod, et al., Example of volume rendering with IMAGEVIS3D of a torso model based on a highresolution CT scan (512!512! 3172 with a voxel size of 0.51x0.51x0.50 mm, courtesy of Siemens Corporate Research, Princeton). By controlling transfer functions, it is possible to identify different systems (e.g. skeleton, vasculature) and organs (e.g. heart) | Figure from R.S. MacLeod, et al., Illustration of simulation of electromagnetic field propagation in a patient-specific brain model. The figure shows a finite-element method discretization of Poissonʼs equation with a patient-specific, five-compartment, geometrical model derived from a segmentation of brain magnetic resonance imaging. The solid lines in the simulation images indicate isopotentials and the small white lines are electrical current streamlines. |
Another component of all our tetrahedral mesh generation pipelines is TETGEN (tetgen.berlios.de), at the moment the most effective and robust open-source tetrahedral mesh generation program, especially for cases with multiple embedded surfaces. It is this ability to deal effectively with the internal boundaries between regions of different characteristics (e.g. electrical conductivity or optical opacity) and to maintain the integrity of outer boundaries, especially when they are concave, which are essential and challenging requirements for applications in biomedicine. Additionally, we recently outlined the details of a new mesh generation tool, BioMesh3D, which includes support for both hexahedral and tetrahedral mesh elements. BioMesh3D makes use of TETGEN and other meshing tools and handles the integration and user interface to modular programs and libraries.
Summary
In many areas of biomedical simulation there is the lack of available software, especially those in the public domain, to carry out all the steps of the simulation pipeline. A major goal of our research and development is to address this need and we have created a set of software tools that support simulation pipelines in at least a few application domains. Wherever possible, we have maintained a high level of generality in the software and the algorithms they combine; however, we propose that, in many situations, there are substantial benefits to adapting software to a particular application that outweighs the resulting inevitable loss of generality. Moreover, by striking a suitable balance between the generality of the simulation pipeline and the specific requirements of a problem domain, our experience suggests that one can achieve another major objective of contemporary biomedical simulation, which is creating subject-specific implementations of clinically relevant numerical simulations.
Associated Publications:
M. Callahan, M.J. Cole, J.F. Shepherd, J.G. Stinstra, C.R. Johnson. "A Meshing Pipeline for Biomedical Models," In Engineering with Computers, Vol. 25, No. 1, Note: DOI:10.1007/s00366-008-0106-1, SpringerLink, pp. 115-130. 2009.R.S. MacLeod, J.G. Stinstra, S. Lew, R.T. Whitaker, D.J. Swenson, M.J. Cole, J. Krueger, D.H. Brooks, C.R. Johnson. "Subject-specific, multiscale simulation of electrophysiology: a software pipeline for image-based models and application examples," In Philosophical Transactions of The Royal Society A, Mathematical, Physical & Engineering Sciences, Vol. 367, No. 1896, pp. 2293--2310. 2009.