Motion Artifacts in Diffusion Imaging

Joint work with: Guido Gerig, Joseph Piven, and Martin Styner

Motivation: Unlike anatomical MRI where subject motion can most often be assessed by quick visual quality control, the detection, characterization and evaluation of the impact of motion in diffusion imaging are challenging issues due to the sensitivity of diffusion weighted imaging (DWI) to motion originating from vibration, cardiac pulsation, breathing and head movement. Post-acquisition motion correction is widely performed, e.g., using the open-source DTIprep software or TORTOISE, but in particular in high angular resolution diffusion imaging (HARDI), users often do not fully understand the consequences of different types of correction schemes on the final analysis, and whether those choices may introduce confounding factors when comparing populations. Although there is excellent theoretical work on the number of directional DWI and its effect on the quality and crossing fiber resolution of orientation distribution functions (ODF), standard users lack clear guidelines and recommendations in practical settings. This research investigates motion correction using transformation and interpolation of affected DWI directions versus the exclusion of subsets of DWI’s, and its effects on diffusion measurements on the reconstructed fiber orientation diffusion functions, on the estimated fiber orientations, and on subsequent tractography and tractography selection. The various effects are systematically studied via 2D and 3D synthetic phantoms and also on real HARDI data.

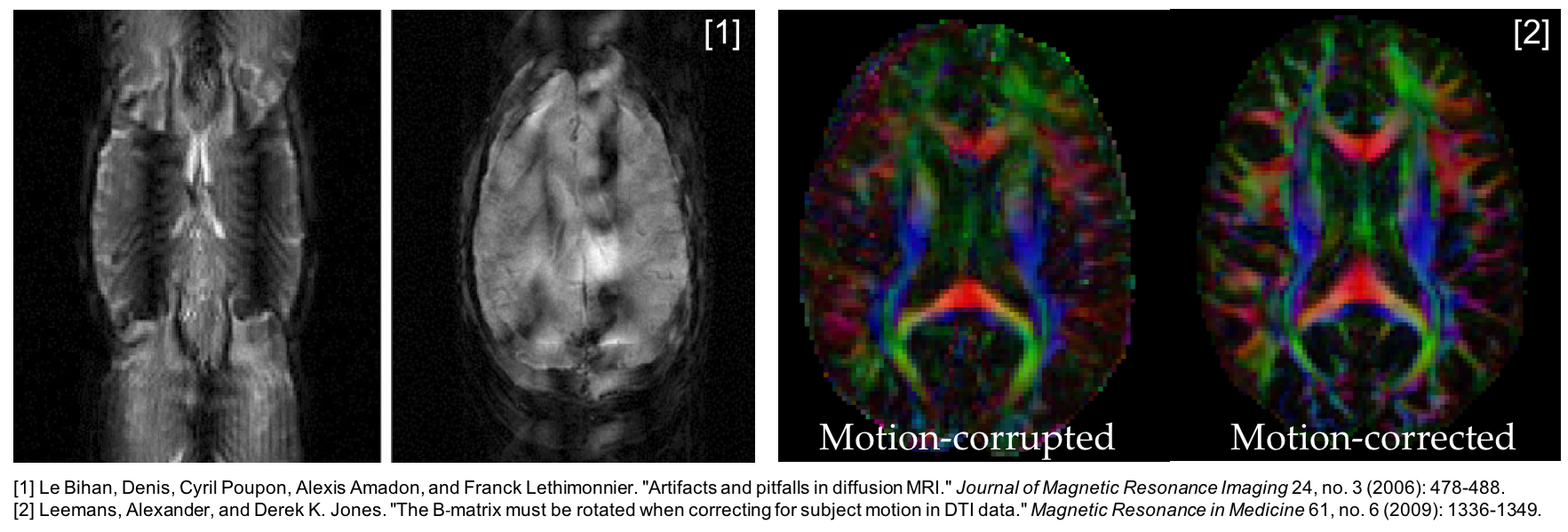
Typical motion artifact: ghosting and large signalvariations across the image.

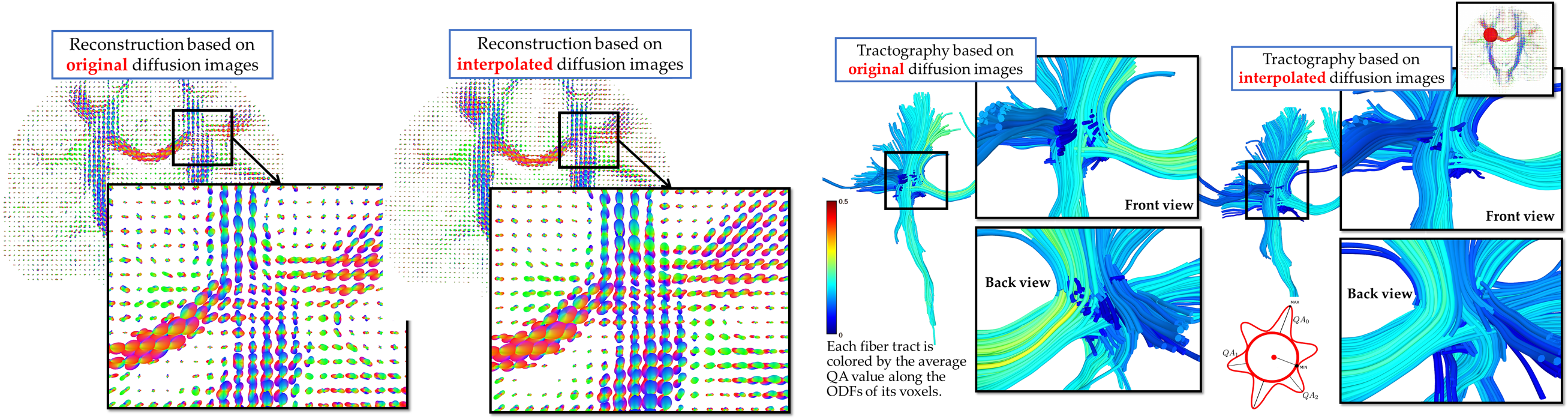
The effects of diffusion interpolation for motion correction on HARDI derived quantities have mostly been disregarded in the scientific community. Nonetheless, the outcomes of a HARDI-based study can significantly vary based on the employed motion correction scheme.

Effects of motion correction were studied on synthetic data and on real HARDI acquisitions. As a proof-of-concept, a 2D synthetic, analytical phantom was constructed including two crossing fiber bundles, a choice of spatial rotation, a user-selected separation angle and generation of diffusion signals following the multi-tensor model with 64 gradient directions and b-value of 3000 s/mm2. Random subject motion was simulated for (30, 50 and 70%) affected gradient directions with random rotations (Normal distribution N(0,5°)). We computed fiber orientation distribution functions (fODFs) based on and calculated fiber orientations following. The real data consisted of two HARDI acquisitions (Siemens Tim Trio, 64DWI, b-value 2000 s/mm2, twice-refocused SE) and subject rotation of about 10° between scans. Considering the first scan as un-corrupted, we replace 30%, 50% and 70% DWIs from the second scan to simulate three scans with different degrees of motion corruption. The impact of motion correction on the estimated fODFs was evaluated a) via Jensen-Shannon divergence (JSD) of the differences between fODF’s, and b) by mean angular deviations of original fiber orientations. Tested scenarios include four image interpolation schemes (nearest neighbor, trilinear, sinc, spline) and removal of bad directions, under 30%, 50% and 70% affected gradient directions.

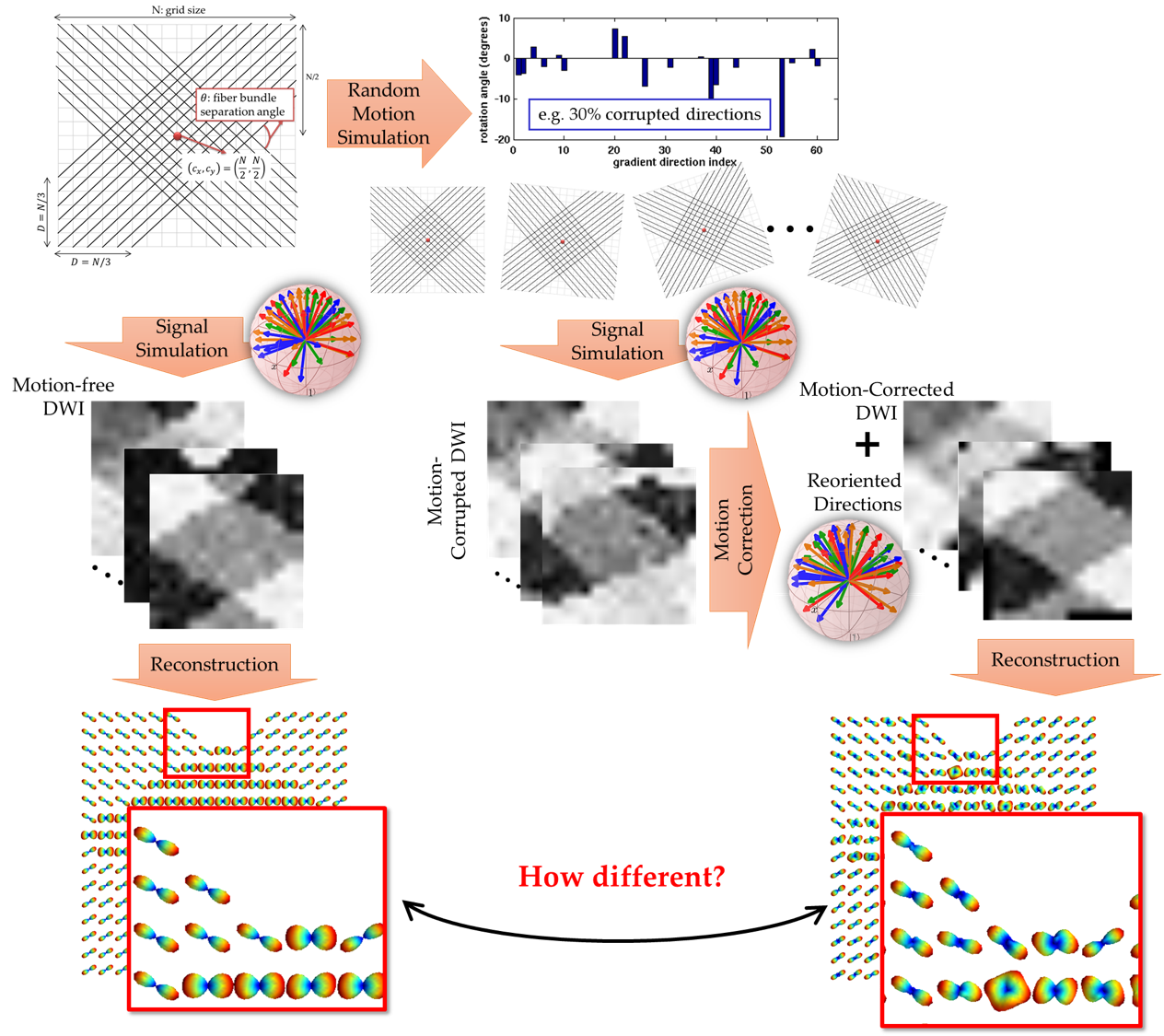
What is the impact of different interpolation schemes, commonly used in motion correction, on the reconstructed fiber orientation distribution functions (fODFs), and the detected fiber orientations ? And what about excluding motion-corrupted DWIs, as an alternative to interpolation?

The consistent findings on real and phantom data confirmed that the simulations reflect well real world scenarios and can therefore be used as a flexible concept to test other combinations of settings adapted to specific clinical studies and available HARDI sequences, and considering motion patterns different from random corruptions. As expected, our analysis did not provide a simple yes/no answer, but did reveal different “best choices” depending on the degree of corruption and other factors. Such evaluations will be critical to optimally adjust settings as available in correction tools such as DTIprep or TORTOISE and thus avoids the current situation where we use pure heuristics, vague assumptions and intuition.

To backup our assumption that motion is omnipresent, we analyze data from three healthy human volunteers (males 30-40 years-old) visiting four clinical sites where they signed a generic consent form at each site agreeing to be scanned for research purposes. The scanning environment was well controlled, a comfortable padding was used to minimize head motion while urging participants to remain without movement. Eddy current was compensated by using a Twice-refocused Spine Echo (TRSE) protocol. The boxplots below show the rotational and translational components of the motion being detected from a total of 24 DWI datasets. This shows an experimental proof of the existence of quantifiable motion (on average 0.4 deg rotation and 0.6 mm translation), even subtle, in the acquired HARDI data. The graphs illustrate the arbitrariness of common calculation of percentage of motion corruption, here shown as a function of thresholding on the estimated motion parameters.

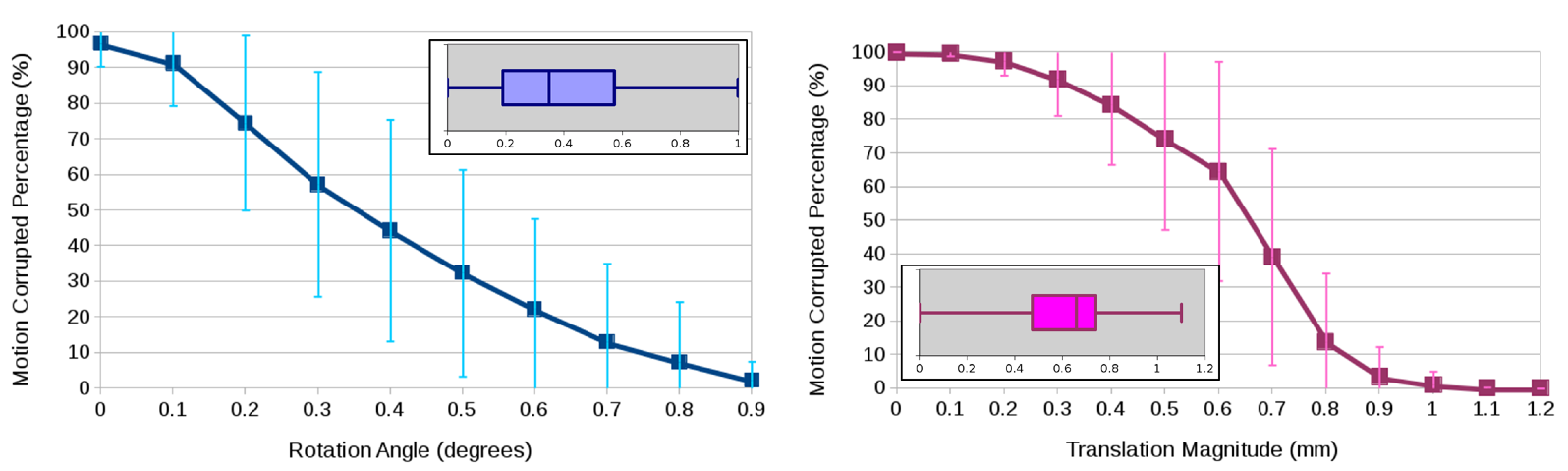
Average and standard deviation of the percentage of motion-corrupted gradient directions as a function of thresholding on the estimated rotation angle in degrees (left) and the estimated translation magnitude in mm (right) for three human phantoms scanned twice at four clinical sites. The boxplots show the overall statistics of estimated motion parameters.

We further extended this evaluation to a comprehensive evaluation framework to systematically assess the outcome of different motion correction choices commonly used by the scientific community on different DWI-derived measures. We made use of human brain HARDI data from a well-controlled motion experiment to simulate various degrees of motion corruption and noise contamination. Choices for correction include exclusion/scrubbing or registration of motion corrupted directions with different choices of interpolation, as well as the option of interpolation of all directions. The comparative evaluation is based on a study of the impact of motion correction using four metrics that quantify (1) similarity of fiber orientation distribution functions (fODFs), (2) deviation of local fiber orientations, (3) global brain connectivity via Graph Diffusion Distance (GDD) and (4) the reproducibility of prominent and anatomically defined fiber tracts. Effects of various motion correction choices are systematically explored and illustrated, leading to a general conclusion of discouraging users from setting ad-hoc thresholds on the estimated motion parameters beyond which volumes are claimed to be corrupted.

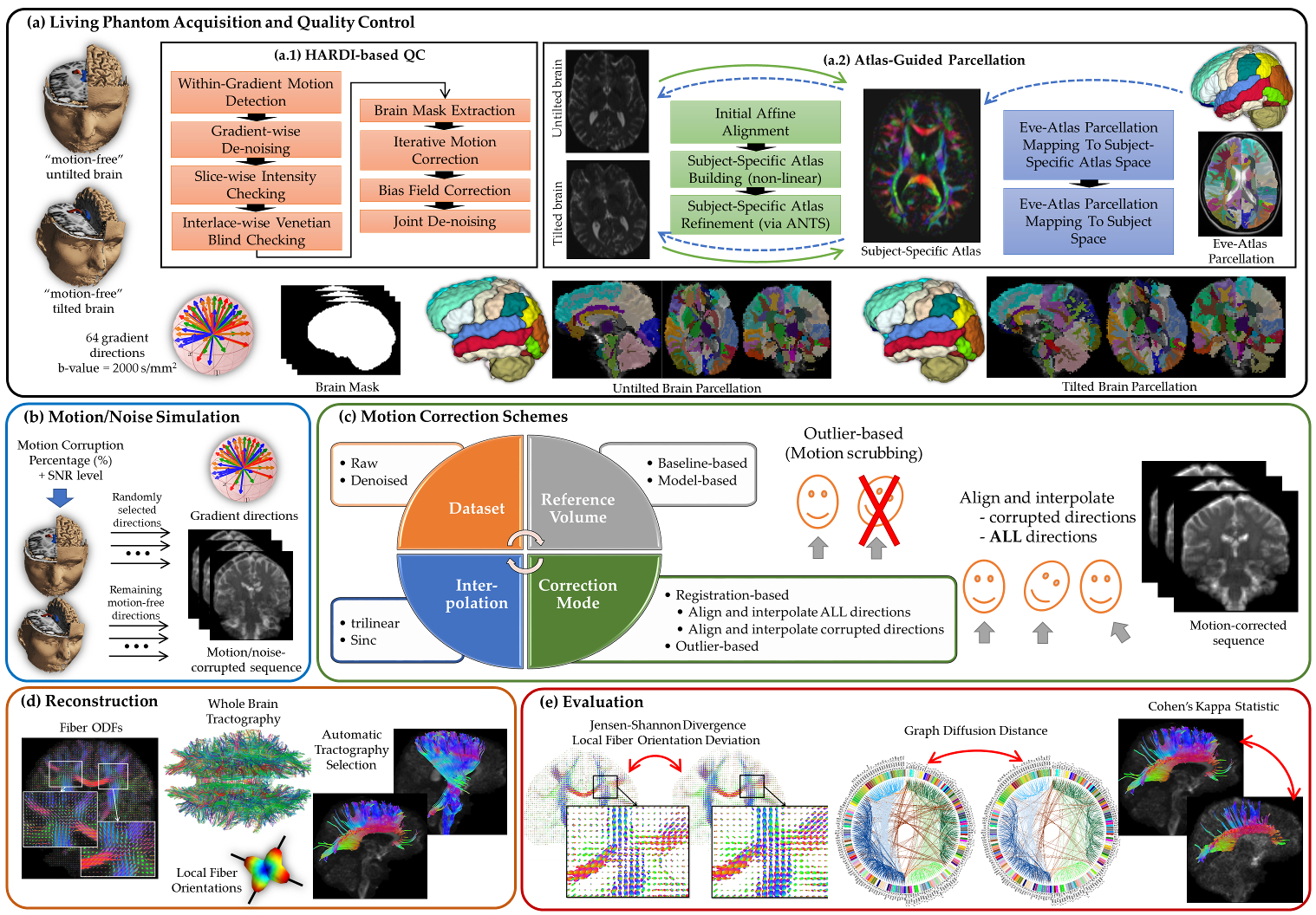
A comprehensive experimental framework for subject motion simulation to systematically evaluate the outcome of different motion correction choices commonly used by the scientific community on HARDI-based reconstructions and tractography. A: A human brain HARDI data was acquired from a well-controlled motion experiment. (a.1) Acquired DWIs were preprocessed to obtain nearly noise-free and motion-free datasets. (a.2) For automated tractography selection and the quantification of whole brain connectivity, a subject-specific unbiased atlas was constructed via DTI-derived data from HARDI sequences resulting in a tensor atlas, where we can define a detailed parcelation of neuroanatomical structures, and map it back to each raw scan. B: Noticeable motion was then simulated by randomly mixing gradients from the acquired datasets. C: Motion correction involves four main decision variables where each distinct combination of choices defines a correction scheme. D: Reconstruction of a corrected or motion-free dataset entails reconstructing the voxel-wise fiber orientation distribution functions, detecting local (voxel-wise) fiber orientation, preforming whole brain tractography and automatically selecting anatomical pathways. E: The evaluation of the effect of a motion correct scheme has been investigated based on voxel-wise metrics, global brain connectivity metric and tract-based metric.

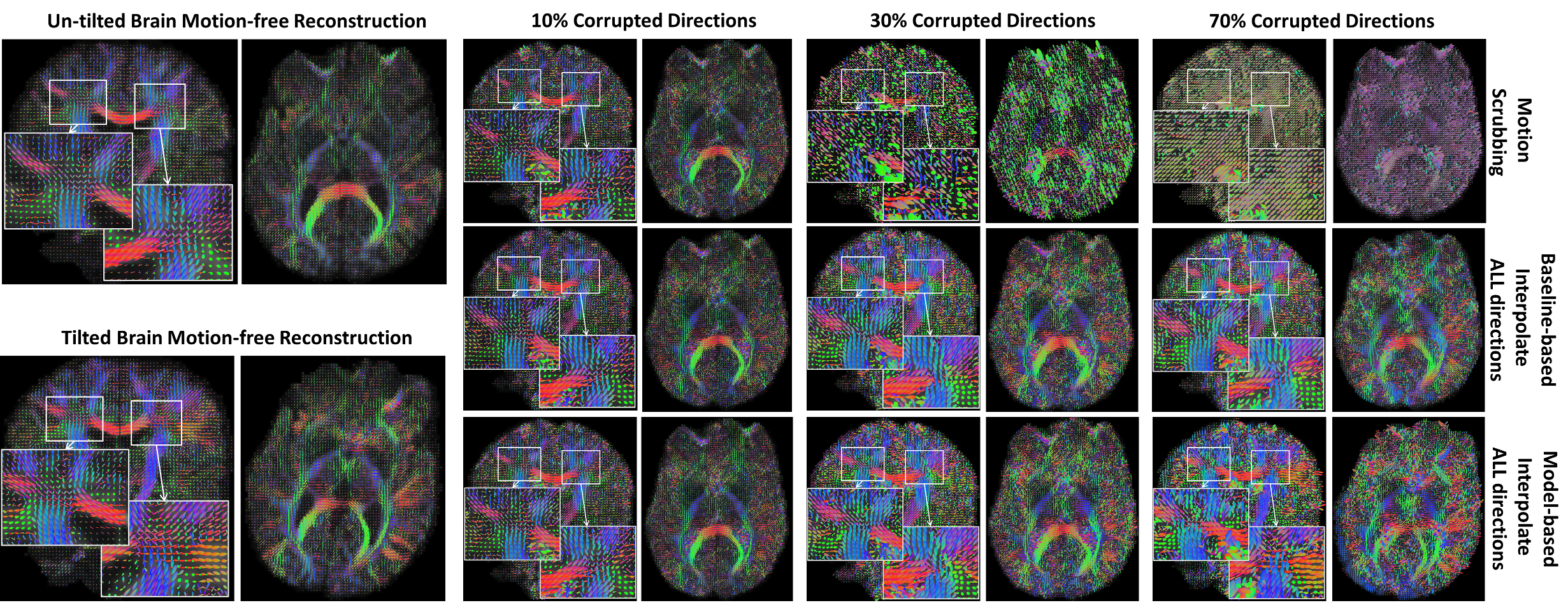
Sample fODFs reconstruction from untilted and tilted motion-free datasets as well as reconstruction from motion-corrected datasets with 10%, 30% and 70% corrupted gradient directions. Correction choices shown include outlier-based (i.e., motion scrubbing) and registration-based (using baseline and model-based reference volumes).

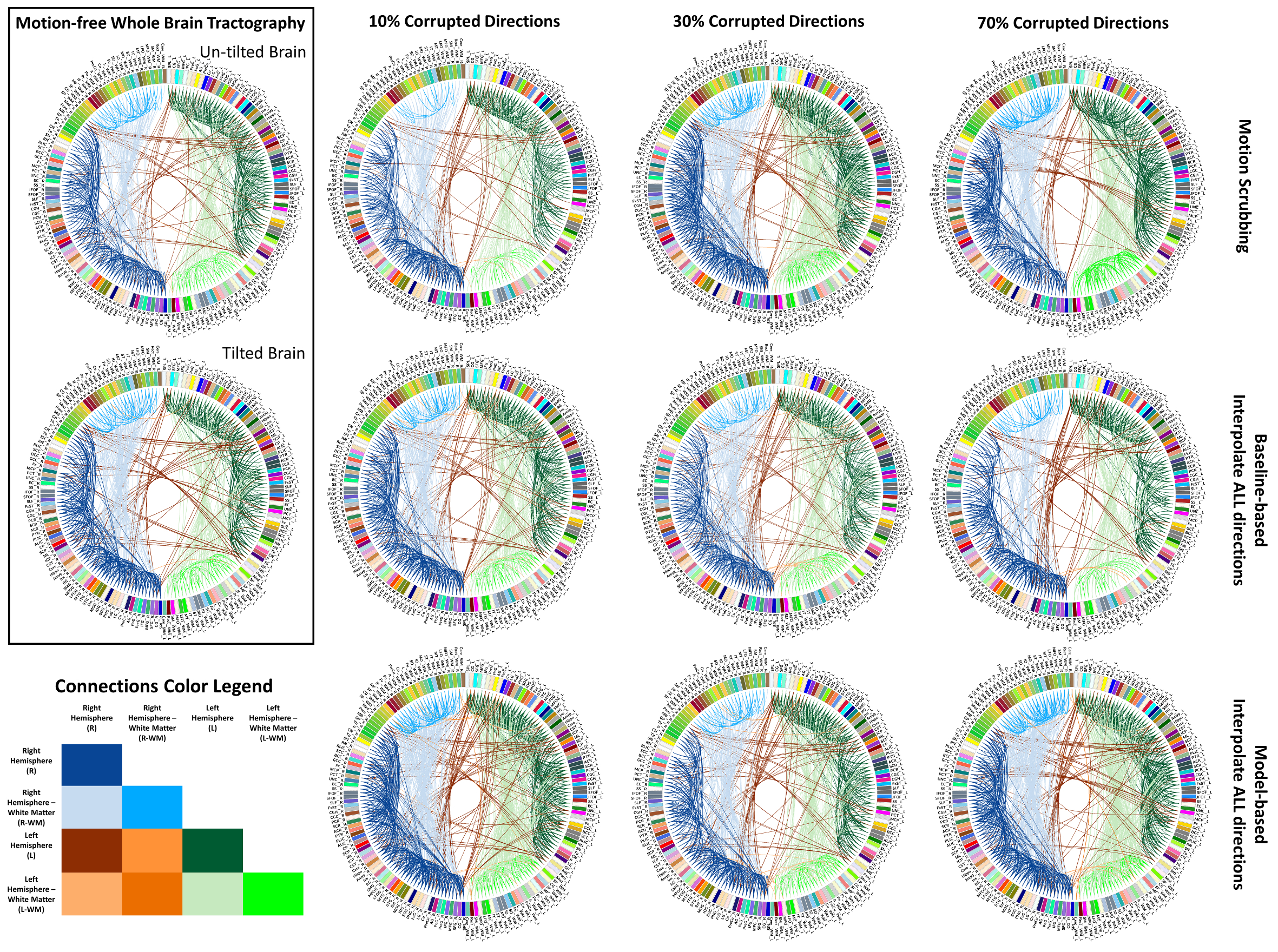
Samplereconstructedconnectomicprofile(i.e.,connectogram)fromuntiltedandtiltedmotion-freedatasetsaswellasconnectogramsfrommotion-corrected datasets with 10%, 30% and 70% corrupted gradient directions. Correction choices shown include outlier-based (i.e., motion scrubbing) and registration-based (using baseline and model-based reference volumes). Notice the tendency of motion scrubbing to add more links between nearby ROIs at corruption percentages, implying the detection of more short tracts.

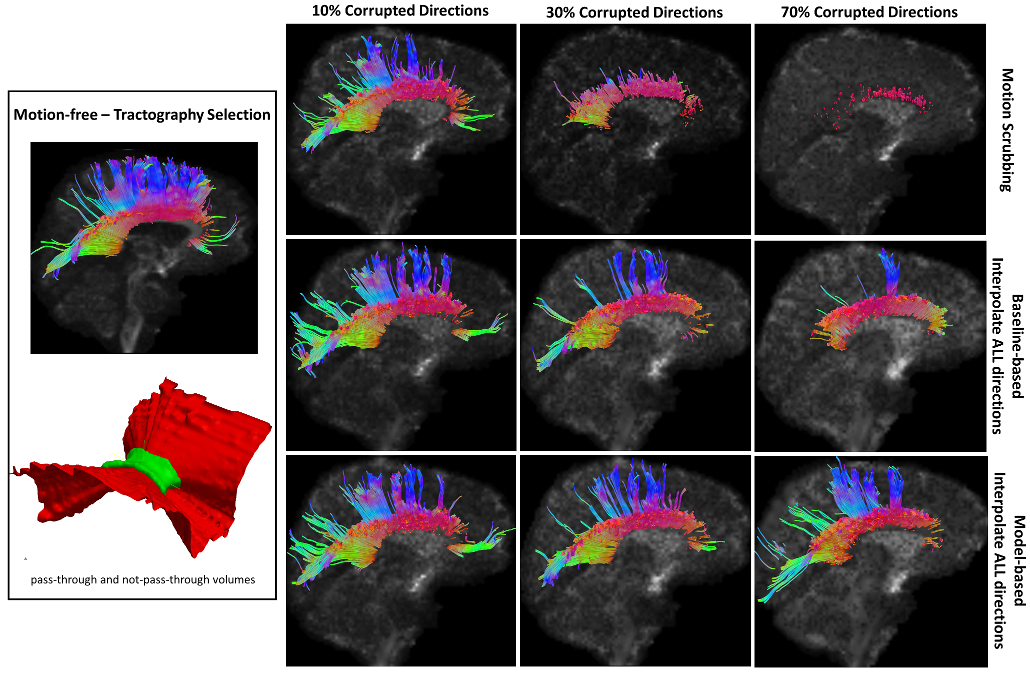
Sample tractography selection for the corpus callosum (CC) from the untilted motion-free dataset as well as selections from motion-corrected datasets with 10%, 30% and 70% corrupted gradient directions. Correction choices shown include outlier-based (i.e., motion scrubbing) and registration-based (using baseline and model-based reference volumes). One can observe the short tracts being detected by motion scrubbing at high corruption percentages due to the exclusion of too many gradient directions.

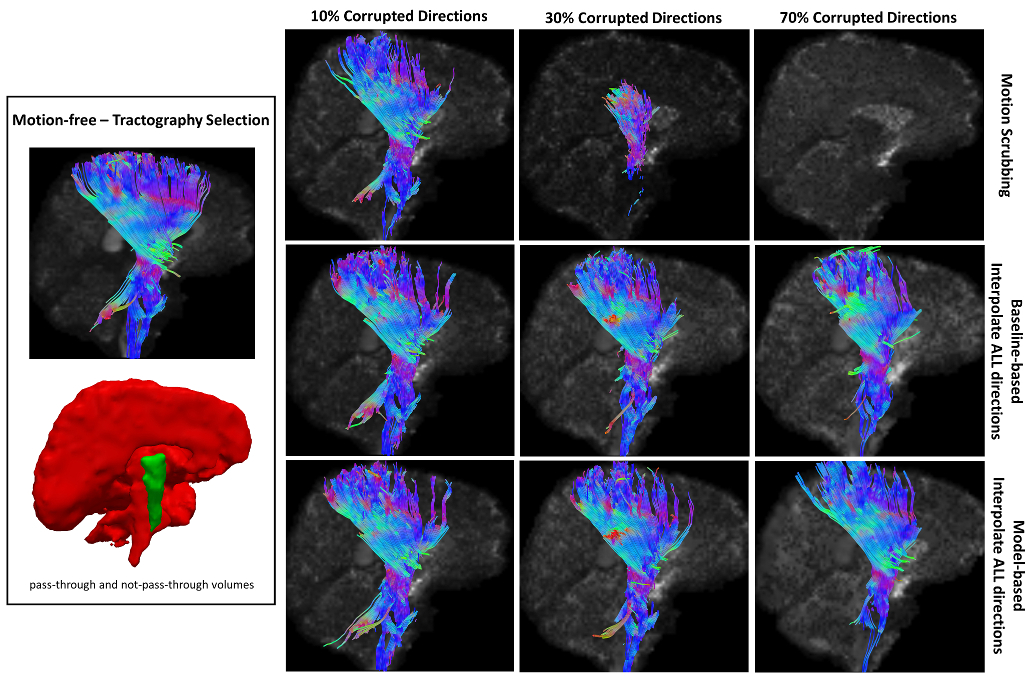
Sample tractography selection for the corticospinal tract (CST) from the untilted motion-free dataset as well as selections from motion-corrected datasets with 10%, 30% and 70% corrupted gradient directions. Correction choices shown include outlier-based (i.e., motion scrubbing) and registration-based (using baseline and model-based reference volumes). Note that motion scrubbing cannot recover long tracts such as CST beyond 10% motion corruption.

Whereas slow bulk motion results in inter-gradient misalignment which can be handled via retrospective motion correction algorithms, fast bulk motion usually affects data during the application of a single diffusion gradient causing signal dropout artifacts. Common practices opt to discard gradients bearing signal attenuation due to the difficulty of their retrospective correction, with the disadvantage to lose full gradients for further processing.

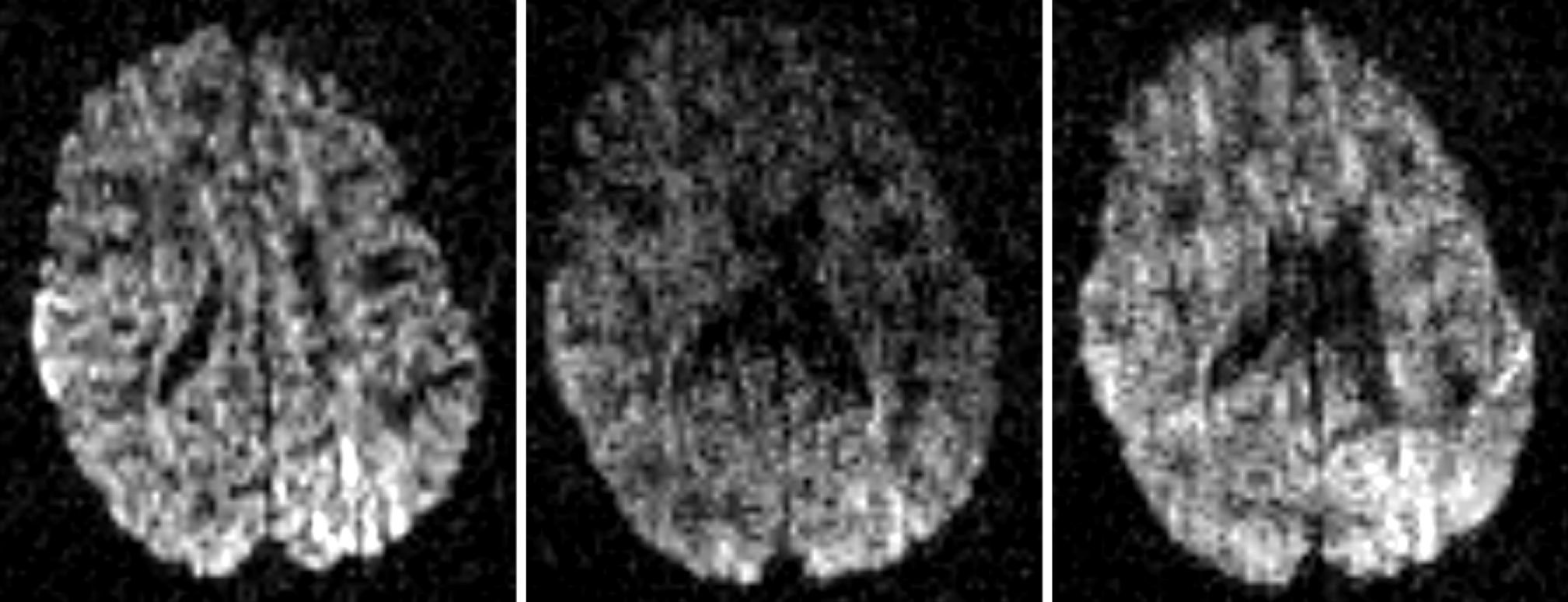
Three consecutive slices in a diffusion gradient suffering from fast bulk motion.

Nonetheless, such attenuation might only affect limited number of slices within a gradient volume. Q-space resampling has recently been proposed to recover corrupted slices while saving gradients for subsequent reconstruction. However, few corrupted gradients are implicitly assumed which might not hold in case of scanning unsedated infants or patients in pain. Instead, we propose to adopt recent advances in compressive sensing based reconstruction of the diffusion orientation distribution functions (ODF) with under sampled measurements to resample corrupted slices. We make use of Simple Harmonic Oscillator based Reconstruction and Estimation (SHORE) basis functions which can analytically model ODF from arbitrary sampled signals. We demonstrate the impact of the proposed resampling strategy compared to state-of-art resampling and gradient exclusion on simulated intra-gradient motion as well as samples from real DWI data.

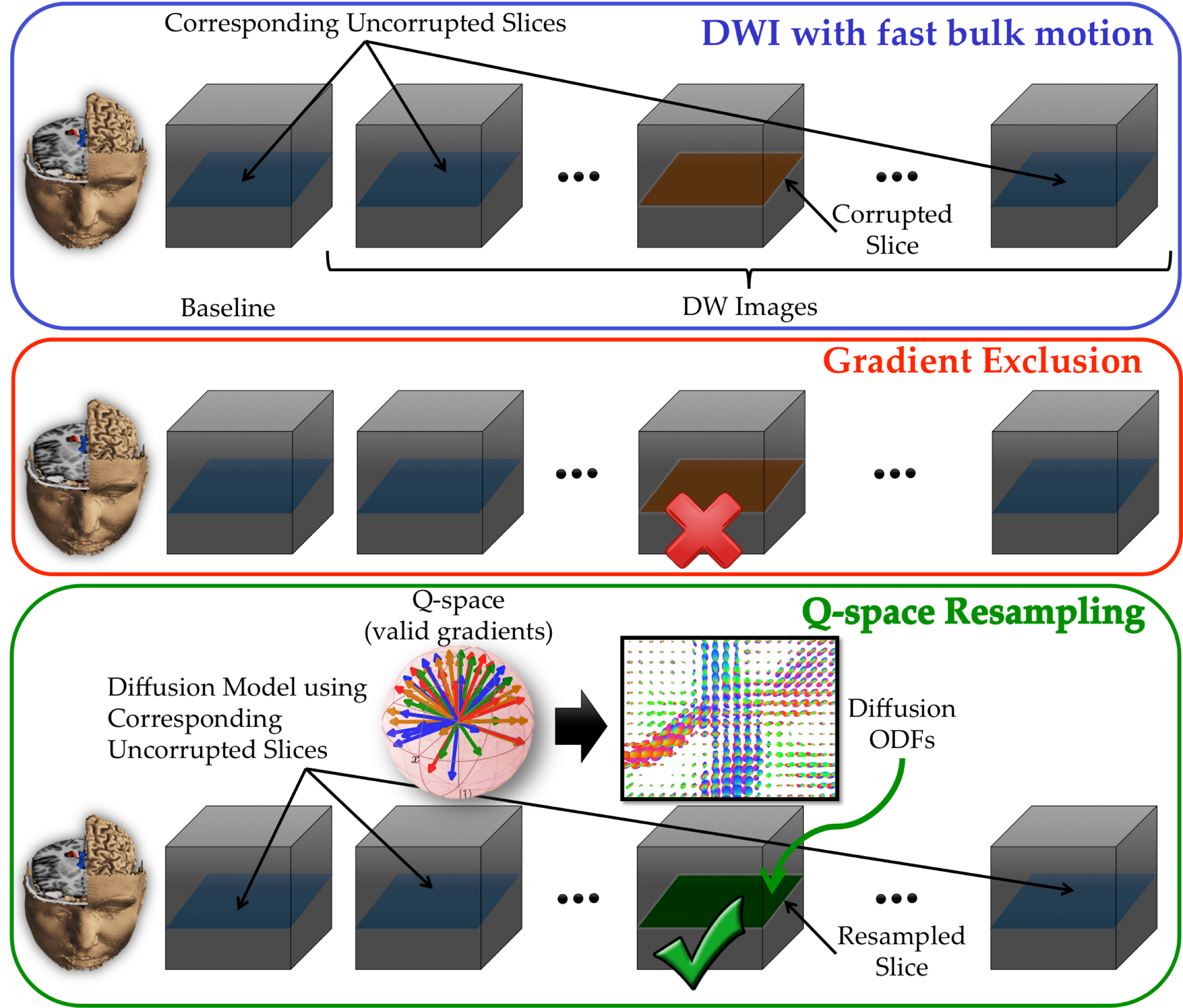
Illustration of q-space resampling strategy compared to gradient exclusion.

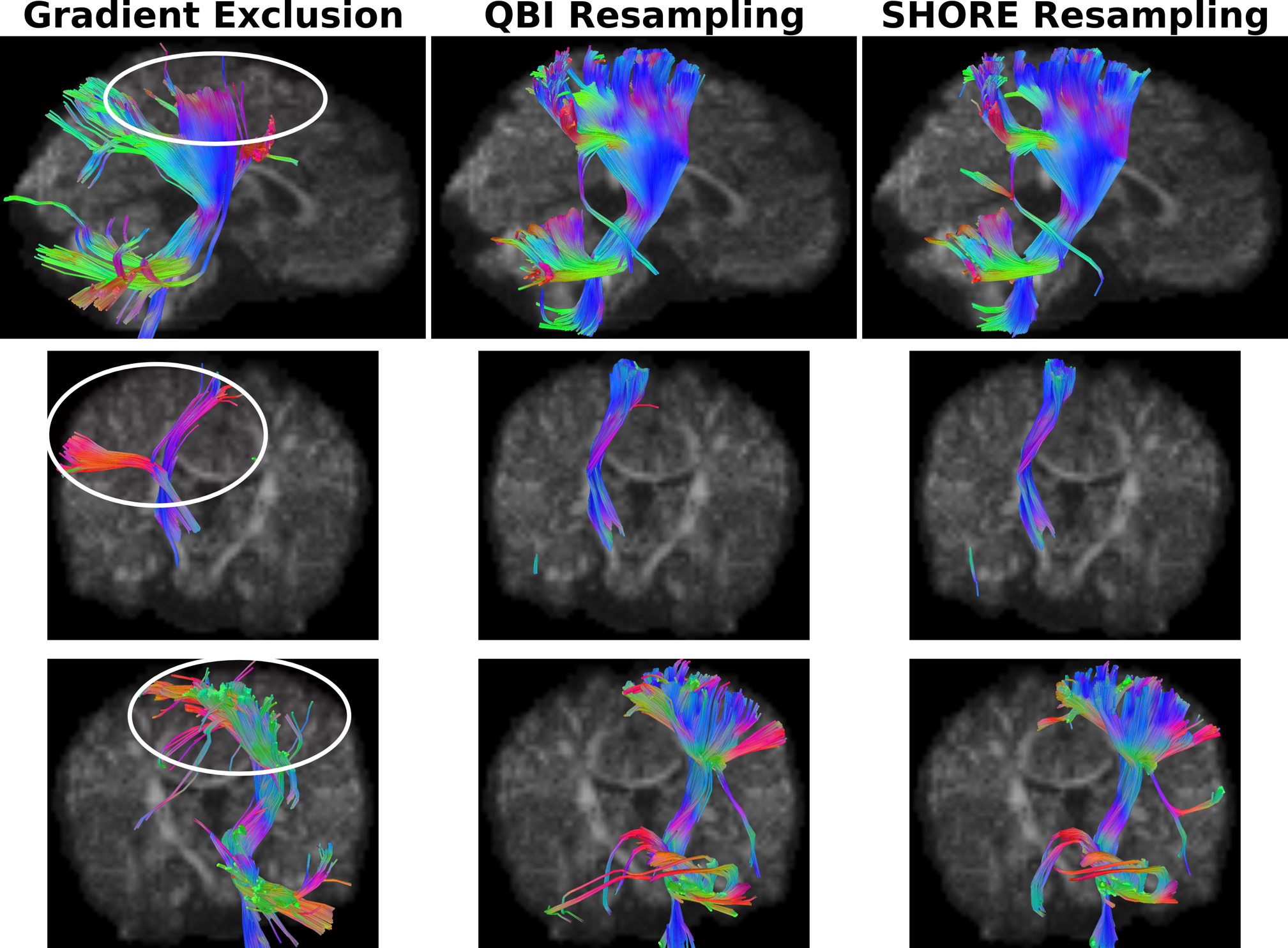
Corticospinal tract of a motion-corrupted infant scan using different reconstruction scenarios. Top row: sagittal view. Middle row: anterior view. Bottom row: posterior view.

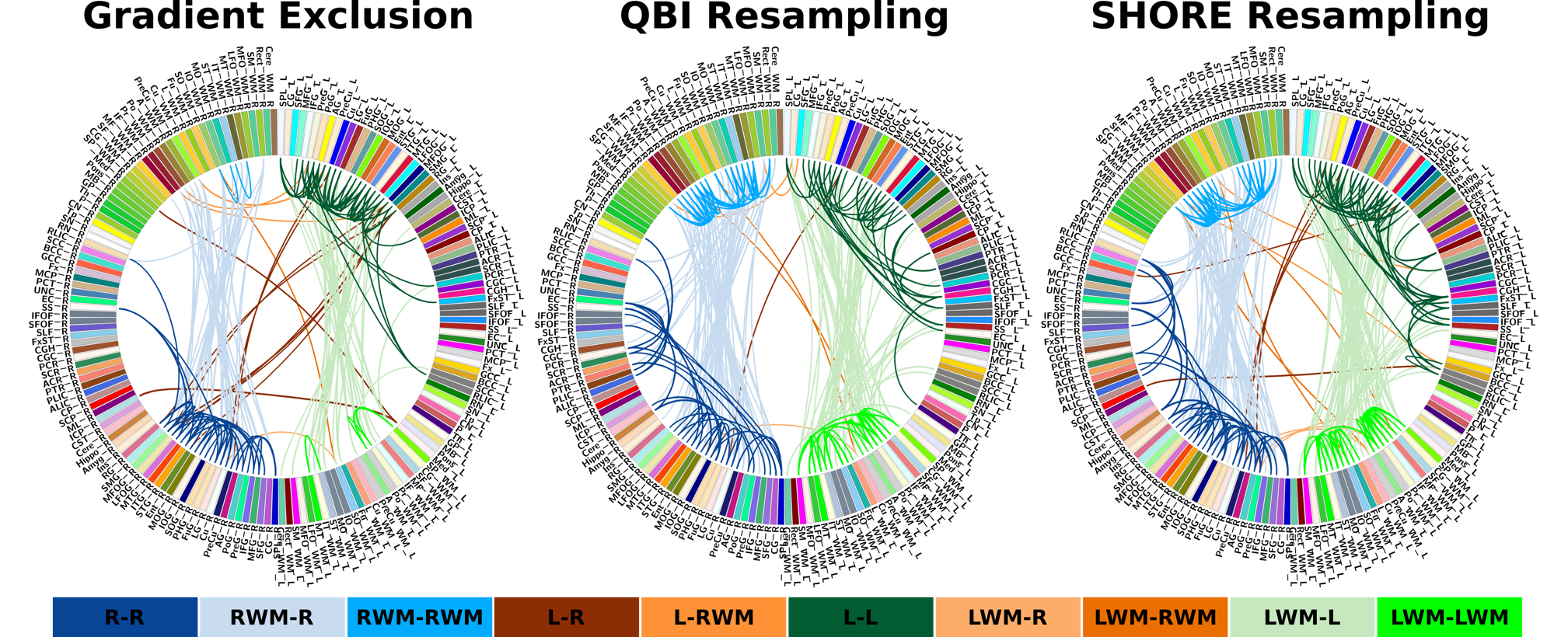
Sample connectomic profile of infant DWI using different reconstruction scenarios. Color legend: L (left), R (right), WM (white matter).

Related publications:

Shireen Y. Elhabian, Clement Vachet, Joseph Piven, Martin Styner, Guido Gerig. Compressive Sensing-based Q-space Resampling for Handling Fast Bulk Motion in HARDI Acquisitions. In IEEE 13th International Symposium of Biomedical Imaging (ISBI), 2016.

Shireen Y. Elhabian, Yaniv Gur, Clement Vachet, Joseph Piven, Martin Styner, Ilana Leppert, G. Bruce Pike, Guido Gerig. Subject-Motion Correction in HARDI Acquisitions: Choices and Consequences. Frontiers in Neurology, 5 (2014): 240.

Shireen Y. Elhabian, Yaniv Gur, Clement Vachet, Joseph Piven, Martin Styner, Ilana Leppert, G. Bruce Pike, Guido Gerig. Motion is Inevitable: The Impact of Motion Correction Schemes on HARDI Reconstructions. MICCAI 2014 Workshop on Computational Diffusion MRI (CDMRI) 2014. pp. 169-179.

Shireen Y. Elhabian, Yaniv Gur, Clement Vachet, Joseph Piven, Martin Styner, Ilana Leppert, G. Bruce Pike, Guido Gerig. A Preliminary Study on the Effect of Motion Correction On HARDI Reconstruction. In Proceedings of the 2014 IEEE International Symposium on Biomedical Imaging (ISBI), 2014, pp. 1055-1058.

Shireen Y. Elhabian, Yaniv Gur, Joseph Piven, Martin Styner, Ilana Leppert, G. Bruce Pike, Guido Gerig. Subject-Motion Correction in HARDI Acquisitions: Choices and Consequences. In Proceeding of the 2014 Joint Annual Meeting ISMRM-ESMRMB, 2014.